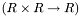KernelExpansion1D< T > Class Template Reference

The base class template for the expansion of $(R \times R \rightarrow R)$-function. More...

#include <FuncExpansion.hpp>

Inheritance diagram for KernelExpansion1D< T >:

Inheritance graph
[legend]
List of all members.

Public Member Functions

virtual T Kernel (T x, T y)=0
 The function to expand.
bool NotInit () const
 Returns true if the basis functions are not set.
T ExpansionValue (T x, T y)
 Computes the linear combination.
T LeftBound () const
 The left bound of the domain.
T RightBound () const
 The right bound of the domain.
void SetBounds (T the_a, T the_b)
 Sets the interval bounds.
int NOfXCoeff () const
 Returns N_1.
int NOfYCoeff () const
 Returns N_2.
 KernelExpansion1D ()
 Constructor.
virtual ~KernelExpansion1D ()
 Virtual destructor.

Public Attributes

ExpansionBasis1D< T > * Phi
ExpansionBasis1D< T > * Psi
SmallMatrix< T > coeff

Protected Attributes

T a
T b

Detailed Description

template<typename T>
class KernelExpansion1D< T >

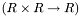The base class template for the expansion of $(R \times R \rightarrow R)$-function.

Constructor & Destructor Documentation

template<typename T>
KernelExpansion1D< T >::KernelExpansion1D (  )  [inline]

Constructor.

Note:
Do not forget to initialize the bounds of the interval before the computation of the expansion coefficients! (Cf. SetBounds .)

template<typename T>
virtual KernelExpansion1D< T >::~KernelExpansion1D (  )  [inline, virtual]

Virtual destructor.

Member Function Documentation

template<typename T>
virtual T KernelExpansion1D< T >::Kernel ( T  x,
T  y 
) [pure virtual]

The function to expand.

Is defined by the user.

Implemented in PrimFuncMthdKernFactor< T >.

template<typename T>
bool KernelExpansion1D< T >::NotInit (  )  const [inline]

Returns true if the basis functions are not set.

template<typename T>
T KernelExpansion1D< T >::ExpansionValue ( T  x,
T  y 
) [inline]

Computes the linear combination.

Parameters:
[in] x Should be in $[a, b]$
[in] y Should be in $[a, b]$
Note:
This is a convinience function only. It allocates memory and therefore can be slow. The function returns the value of the linear combination at the given point

template<typename T>
T KernelExpansion1D< T >::LeftBound (  )  const [inline]

The left bound of the domain.

template<typename T>
T KernelExpansion1D< T >::RightBound (  )  const [inline]

The right bound of the domain.

template<typename T>
void KernelExpansion1D< T >::SetBounds ( T  the_a,
T  the_b 
) [inline]

Sets the interval bounds.

Parameters:
[in] the_a The bounds
[in] the_b The bounds
Note:
You should not change the bounds after the expansion is initialized!

template<typename T>
int KernelExpansion1D< T >::NOfXCoeff (  )  const [inline]

Returns N_1.

template<typename T>
int KernelExpansion1D< T >::NOfYCoeff (  )  const [inline]

Returns N_2.

Member Data Documentation

template<typename T>
T KernelExpansion1D< T >::a [protected]

template<typename T>
T KernelExpansion1D< T >::b [protected]

The domain of the function is $[a, b] \times [a, b]$

template<typename T>
ExpansionBasis1D<T>* KernelExpansion1D< T >::Phi

The basis functions on $[0, 1]$ for the x-direction

template<typename T>
ExpansionBasis1D<T>* KernelExpansion1D< T >::Psi

The basis functions on $[0, 1]$ for the y-direction

template<typename T>
SmallMatrix<T> KernelExpansion1D< T >::coeff

The coefficients

The documentation for this class was generated from the following file:
Generated on Fri Sep 21 12:34:15 2007 for SG2 by  doxygen 1.5.2