small_matrix< T > Class Template Reference

The low-level class for small dense matrices. More...

#include <small_matrix.hpp>

Inheritance diagram for small_matrix< T >:

Inheritance graph
[legend]
List of all members.

Public Member Functions

 small_matrix ()
 Empty constructor.
void init (int the_m, int the_n, T *the_entries)
 Initializes the fields of the structure.
 small_matrix (int the_m, int the_n, T *the_entries)
 Creates a small matrix of a given size.
 small_matrix (int the_m, int the_n, T &first_entry)
 Creates a small matrix of a given size.
 small_matrix (int the_m, T *the_entries)
 Creates a small VECTOR (NOT a square matrix).
 small_matrix (int the_m, T &first_entry)
 Creates a small VECTOR (NOT a square matrix).
int n_rows () const
 Returns the number of the rows.
int n_cols () const
 Returns the number of the columns.
T * entries ()
 Pointer to the array of the entries.
const T * entries () const
 Const-pointer to the array of the entries.
bool has_size (int the_m, int the_n=1) const
 Checks the matrix size.
bool has_same_size_as (const small_matrix< T > &A) const
 Checks whether 'this' matrix has the same size as A.
bool is_mul_compatible_with (const small_matrix< T > &A) const
 Non-zero if 'this * A' is well-defined.
void print_maple (std::ostream &s) const
 Prints the matrix in the Maple form.
void print_matlab (std::ostream &s) const
 Prints in the Matlab form.
const T & operator() (int i, int j) const
 Const indexation of the matrix entries.
T & operator() (int i, int j)
 Indexation of the matrix entries.
const T & operator() (int i) const
 Const indexation operator for vectors.
T & operator() (int i)
 Indexation operator for vectors.
small_matrix< T > & operator= (const small_matrix< T > &from)
 Assignment operator.
small_matrix< T > & operator= (const T *seg)
 Copying the entries from a memory segment.
small_matrix< T > & zero ()
 Set all the entries to zero.
small_matrix< T > & diag (T a)
 Number-to-matrix assignment: 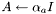$ A \leftarrow \alpha_{a} I$.
double norm2 () const
 The vector Eucleadean norm.
double max_norm () const
 The maximum vector norm.
double norm1 () const
 The Frobenius norm.
T trace () const
 Returns the trace of a SQUARE matrix: 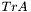$ Tr A$.
T compute_det ()
 Computes the determinant of 'this' matrix: 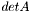$ det A$.
T operator & (small_matrix< T > &vec) const
 Scalar product (the sum of the products)$v_{this} \cdot w_{vec}$.
small_matrix< T > & operator *= (T scalar)
 Multiply 'this' matrix by a scalar 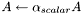$ A \leftarrow \alpha_{scalar} A$.
small_matrix< T > & operator/= (T scalar)
 Divide 'this' matrix by a scalar: $ A \leftarrow \frac{1}{\alpha_{scalar}} A$.
small_matrix< T > & product (T scalar, const small_matrix< T > &A)
 Multiply a matrix by a scalar and save the result in 'this' matrix: 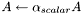$ A \leftarrow \alpha_{scalar} A$.
small_matrix< T > & product (const small_matrix< T > &A, T scalar)
 Multiply a matrix by a scalar and save the result in 'this' matrix: $ C_{this} \leftarrow \alpha_{scalar} A$.
small_matrix< T > & add_mul (T scalar, const small_matrix< T > &A)
 Multiply a matrix by a scalar and add the result to 'this': $ C_{this} \leftarrow C_{this} + \alpha_{scalar} A$.
small_matrix< T > & add_mul (const small_matrix< T > &A, T scalar)
 Multiply a matrix by a scalar and add the result to 'this': $ C_{this} \leftarrow C_{this} + \alpha_{scalar} A$.
small_matrix< T > & sum (const small_matrix< T > &A, const small_matrix< T > &B)
 Add two matrices and save the result in 'this' one: $ C_{this} \leftarrow A + B$.
small_matrix< T > & operator+= (const small_matrix< T > &A)
 Add matrix to 'this' one: 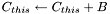$ C_{this} \leftarrow C_{this} + B$.
small_matrix< T > & difference (const small_matrix< T > &A, const small_matrix< T > &B)
 Subtract one matrix from another and save the result in 'this' one: $ C_{this} \leftarrow A - B$.
small_matrix< T > & operator-= (const small_matrix< T > &A)
 Subtract matrix from'this' one: $ C_{this} \leftarrow C_{this} - B$.
small_matrix< T > & product (const small_matrix< T > &A, const small_matrix< T > &B)
 Multiply two matrices and save the result in 'this' one: 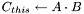$ C_{this} \leftarrow A \cdot B$.
small_matrix< T > & add_mul (const small_matrix< T > &A, const small_matrix< T > &B)
 Multiply two matrices and save the result in 'this' one: $ C_{this} \leftarrow C_{this} + A \cdot B$.
small_matrix< T > & sub_mul (small_matrix< T > &A, small_matrix< T > &B)
 Operation $ C_{this} \leftarrow C_{this} - A \cdot B$.
small_matrix< T > & add_a_mul (T a, small_matrix< T > &A, small_matrix< T > &B)
 Operation 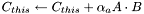$ C_{this} \leftarrow C_{this} + \alpha_{a} A \cdot B$.
small_matrix< T > & transposed (small_matrix< T > &A)
 Transpose a given matrix and save the result to 'this' one: 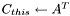$ C_{this} \leftarrow A^{T}$.
small_matrix< T > & transposed ()
 Transposes 'this' matrix: $ C_{this} \leftarrow C_{this}^{T} $.
small_matrix< T > & conjugate (small_matrix< T > &A)
 Compute the conjugate of a given matrix and save the result to 'this' one: 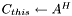$ C_{this} \leftarrow A^{H}$.
small_matrix< T > & conjugate ()
 Computes a conjugate of 'this' matrix, returns the reference to it: 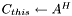$ C_{this} \leftarrow A^{H}$.
small_matrix< T > & invmul_Gauss (small_matrix< T > &M1)
 Operation: 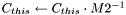$ C_{this} \leftarrow C_{this}\cdot M2^{-1}$.
void LU_decomp (small_matrix< T > *inv_L=0)
 Computes the complete LU-decomposition of a matrix, i. e. :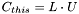$ C_{this} = L \cdot U$.
small_matrix< T > & mul_by_Givens (small_matrix< T > &M1)
 Multiply 'this' matrix (M2) by the Givens rotation transforming a given matrix (M1) to an upper triangular form.
small_matrix< T > & invmul_Givens (small_matrix< T > &M1)
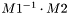 Multiplyes 'this' (M2) matrix by $M1^{-1}$, thus computes the product $M1^{-1} \cdot M2$.
void QR_Givens (small_matrix< T > &M)
 Computes the QR-decomposition by the Givens rotations.
template<>
float conj (float x)
template<>
double abs (float x)
template<>
double sc_square (float x)
template<>
bool is_num_zero (float x)

Static Public Member Functions

static T conj (T x)
static double abs (T x)
static bool is_num_zero (T x)
static double sc_square (T x)

Protected Attributes

int m
int n
T * entry

Detailed Description

template<class T>
class small_matrix< T >

The low-level class for small dense matrices.

No implicit dynamic memory allocation.

Constructor & Destructor Documentation

template<class T>
small_matrix< T >::small_matrix (  )  [inline]

Empty constructor.

We allow dummy objects.

template<class T>
small_matrix< T >::small_matrix ( int  the_m,
int  the_n,
T *  the_entries 
) [inline]

Creates a small matrix of a given size.

Parameters:
[in] the_m The horizontal size of the matrix.
[in] the_n The vertical size of the matrix.
[in] the_entries Array of entries.

template<class T>
small_matrix< T >::small_matrix ( int  the_m,
int  the_n,
T &  first_entry 
) [inline]

Creates a small matrix of a given size.

The same but with "T &" instead of "T *"

Parameters:
[in] the_m The horizontal size of the matrix.
[in] the_n The vertical size of the matrix.
[in] first_entry Reference of the first entry.

template<class T>
small_matrix< T >::small_matrix ( int  the_m,
T *  the_entries 
) [inline]

Creates a small VECTOR (NOT a square matrix).

Parameters:
[in] the_m The size.
[in] the_entries The array of entries.

template<class T>
small_matrix< T >::small_matrix ( int  the_m,
T &  first_entry 
) [inline]

Creates a small VECTOR (NOT a square matrix).

The same but with "T &" instead of "T *"

Parameters:
[in] the_m the size
[in] first_entry reference of the first entry

Member Function Documentation

template<class T>
static T small_matrix< T >::conj ( T  x  )  [static]

the conjugate of x

template<class T>
static double small_matrix< T >::abs ( T  x  )  [static]

the absolute value of x

template<class T>
static bool small_matrix< T >::is_num_zero ( T  x  )  [static]

true if x is numerically zero

template<class T>
static double small_matrix< T >::sc_square ( T  x  )  [static]

returns x * conj (x)

template<class T>
void small_matrix< T >::init ( int  the_m,
int  the_n,
T *  the_entries 
) [inline]

Initializes the fields of the structure.

Parameters:
[in] the_m The horizontal size of the matrix.
[in] the_n The vertical size of the matrix.
[in] the_entries Array of entries.

template<class T>
int small_matrix< T >::n_rows (  )  const [inline]

Returns the number of the rows.

template<class T>
int small_matrix< T >::n_cols (  )  const [inline]

Returns the number of the columns.

template<class T>
T* small_matrix< T >::entries (  )  [inline]

Pointer to the array of the entries.

template<class T>
const T* small_matrix< T >::entries (  )  const [inline]

Const-pointer to the array of the entries.

template<class T>
bool small_matrix< T >::has_size ( int  the_m,
int  the_n = 1 
) const [inline]

Checks the matrix size.

Parameters:
[in] the_m The true size.
[in] the_n The true size.
Returns:
true if the m- and n-size of the matrix is the same as the given one, false otherwise.

template<class T>
bool small_matrix< T >::has_same_size_as ( const small_matrix< T > &  A  )  const [inline]

Checks whether 'this' matrix has the same size as A.

template<class T>
bool small_matrix< T >::is_mul_compatible_with ( const small_matrix< T > &  A  )  const [inline]

Non-zero if 'this * A' is well-defined.

template<class T>
void small_matrix< T >::print_maple ( std::ostream &  s  )  const

Prints the matrix in the Maple form.

Reimplemented in small_vector< T >, and small_vector< double >.

template<class T>
void small_matrix< T >::print_matlab ( std::ostream &  s  )  const

Prints in the Matlab form.

template<class T>
const T& small_matrix< T >::operator() ( int  i,
int  j 
) const [inline]

Const indexation of the matrix entries.

This operation allows to index the matrix entries starting from (0, 0). Example: M (1, 0) means the first entry in the second line.

Parameters:
[in] i Row-index of the element.
[in] j Column-index of the element.

template<class T>
T& small_matrix< T >::operator() ( int  i,
int  j 
) [inline]

Indexation of the matrix entries.

This operation allows to index the matrix entries starting from (0, 0). Example: M (1, 0) means the first entry in the second line.

Parameters:
[in] i Row-index of the element.
[in] j Column-index of the element.

template<class T>
const T& small_matrix< T >::operator() ( int  i  )  const [inline]

Const indexation operator for vectors.

E. g. vec (3) means the third 4th component of 'vec'.

Parameters:
[in] i Index of the element.

template<class T>
T& small_matrix< T >::operator() ( int  i  )  [inline]

Indexation operator for vectors.

E. g. vec (3) means the third 4th component of 'vec'.

Parameters:
[in] i Index of the element.

template<class T>
small_matrix< T > & small_matrix< T >::operator= ( const small_matrix< T > &  from  )  [inline]

Assignment operator.

Merely copies the entries of the source matrix to the entries of the destination matrix. The matrices should have the same size.

Parameters:
[in] from Source matrix.

template<class T>
small_matrix<T>& small_matrix< T >::operator= ( const T *  seg  )  [inline]

Copying the entries from a memory segment.

Merely copies n * m values starting from a given pointer to the entry array.

template<class T>
small_matrix<T>& small_matrix< T >::zero (  )  [inline]

Set all the entries to zero.

template<class T>
small_matrix< T > & small_matrix< T >::diag ( T  a  )  [inline]

Number-to-matrix assignment: 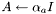$ A \leftarrow \alpha_{a} I$.

Sets the matrix to a I for a given scalar a. The matrix should be square.

template<class T>
double small_matrix< T >::norm2 (  )  const [inline]

The vector Eucleadean norm.

template<class T>
double small_matrix< T >::max_norm (  )  const [inline]

The maximum vector norm.

template<class T>
double small_matrix< T >::norm1 (  )  const [inline]

The Frobenius norm.

template<class T>
T small_matrix< T >::trace (  )  const [inline]

Returns the trace of a SQUARE matrix: 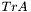$ Tr A$.

The matrix should be square.

template<class T>
T small_matrix< T >::compute_det (  )  [inline]

Computes the determinant of 'this' matrix: 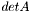$ det A$.

The function returns the value of the determinant. The 'this' matrix must be square. During the computation, 'this' matrix is DESTROYED.

Note:
Currently the Givens rotations are used to compute the almost upper triangular matrix. Only the last two rows correspond to the block-tridiagonal matrix with the diagonal 2x2-block. The determinant is then the product of the determinant of this block and the diagonal entries.

template<class T>
T small_matrix< T >::operator & ( small_matrix< T > &  vec  )  const [inline]

Scalar product (the sum of the products)$v_{this} \cdot w_{vec}$.

Parameters:
[in] vec The second argument of the product.
Returns:
The scalar-product.

template<class T>
small_matrix<T>& small_matrix< T >::operator *= ( T  scalar  )  [inline]

Multiply 'this' matrix by a scalar 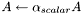$ A \leftarrow \alpha_{scalar} A$.

template<class T>
small_matrix<T>& small_matrix< T >::operator/= ( T  scalar  )  [inline]

Divide 'this' matrix by a scalar: $ A \leftarrow \frac{1}{\alpha_{scalar}} A$.

template<class T>
small_matrix<T>& small_matrix< T >::product ( T  scalar,
const small_matrix< T > &  A 
) [inline]

Multiply a matrix by a scalar and save the result in 'this' matrix: 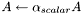$ A \leftarrow \alpha_{scalar} A$.

The size of a source matrix should correspond to the size of 'this' matrix.

Parameters:
[in] scalar The scalar by which the matrix shall be multiplied.
[in,out] A The matrix that shall be multiplied.
Returns:
Reference to the multiplied matrix.

template<class T>
small_matrix<T>& small_matrix< T >::product ( const small_matrix< T > &  A,
T  scalar 
) [inline]

Multiply a matrix by a scalar and save the result in 'this' matrix: $ C_{this} \leftarrow \alpha_{scalar} A$.

The size of a source matrix should correspond to the size of 'this' matrix.

Parameters:
[in] scalar The scalar by which the matrix shall be multiplied.
[in,out] A The matrix that shall be multiplied.
Returns:
Reference to the multiplied matrix.

template<class T>
small_matrix<T>& small_matrix< T >::add_mul ( T  scalar,
const small_matrix< T > &  A 
) [inline]

Multiply a matrix by a scalar and add the result to 'this': $ C_{this} \leftarrow C_{this} + \alpha_{scalar} A$.

The size of a source matrix should correspond to the size of 'this' matrix.

Parameters:
[in] scalar The scalar by which the matrix shall be multiplied.
[in,out] A The matrix that shall be multiplied.
Returns:
Reference to the multiplied matrix.

template<class T>
small_matrix<T>& small_matrix< T >::add_mul ( const small_matrix< T > &  A,
T  scalar 
) [inline]

Multiply a matrix by a scalar and add the result to 'this': $ C_{this} \leftarrow C_{this} + \alpha_{scalar} A$.

The size of a source matrix should correspond to the size of 'this' matrix.

Parameters:
[in] scalar The scalar by which the matrix shall be multiplied.
[in,out] A The matrix that shall be multiplied.
Returns:
Reference to the multiplied matrix.

template<class T>
small_matrix< T > & small_matrix< T >::sum ( const small_matrix< T > &  A,
const small_matrix< T > &  B 
) [inline]

Add two matrices and save the result in 'this' one: $ C_{this} \leftarrow A + B$.

All the matrices should have equal sizes. The matrices may not be different. The function returns the reference to 'this' object.

Parameters:
[in] A Left-hand side
[in] B Right-hand side
Returns:
Reference to A

template<class T>
small_matrix<T>& small_matrix< T >::operator+= ( const small_matrix< T > &  A  )  [inline]

Add matrix to 'this' one: 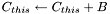$ C_{this} \leftarrow C_{this} + B$.

All the matrices should have equal sizes. The matrices may not be different.

Parameters:
[in] A Right-hand side
Returns:
Reference to this

template<class T>
small_matrix< T > & small_matrix< T >::difference ( const small_matrix< T > &  A,
const small_matrix< T > &  B 
) [inline]

Subtract one matrix from another and save the result in 'this' one: $ C_{this} \leftarrow A - B$.

All the matrices should have equal sizes. The matrices may not be different.

Parameters:
[in] A Left-hand side
[in] B Right-hand side
Returns:
Reference to A

template<class T>
small_matrix<T>& small_matrix< T >::operator-= ( const small_matrix< T > &  A  )  [inline]

Subtract matrix from'this' one: $ C_{this} \leftarrow C_{this} - B$.

All the matrices should have equal sizes. The matrices may not be different.

Parameters:
[in] A Right-hand side
Returns:
Reference to this

template<class T>
small_matrix< T > & small_matrix< T >::product ( const small_matrix< T > &  A,
const small_matrix< T > &  B 
) [inline]

Multiply two matrices and save the result in 'this' one: 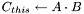$ C_{this} \leftarrow A \cdot B$.

The sizes of the matrices should be 'consistent'. The arguments may coincide, but should not coinside with 'this' matrix.

Parameters:
[in] A Left-hand side
[in] B Right-hand side
Returns:
Reference to C

template<class T>
small_matrix< T > & small_matrix< T >::add_mul ( const small_matrix< T > &  A,
const small_matrix< T > &  B 
) [inline]

Multiply two matrices and save the result in 'this' one: $ C_{this} \leftarrow C_{this} + A \cdot B$.

The sizes of the matrices should be 'consistent'. The arguments may coincide, but should not coinside with 'this' matrix.

Parameters:
[in] A Left-hand side
[in] B Right-hand side
Returns:
Reference to C

template<class T>
small_matrix< T > & small_matrix< T >::sub_mul ( small_matrix< T > &  A,
small_matrix< T > &  B 
) [inline]

Operation $ C_{this} \leftarrow C_{this} - A \cdot B$.

The matrices should have the consistent sizes. A and B may coincide, but may not coincide with *this. The function returns the reference to 'this'.

template<class T>
small_matrix< T > & small_matrix< T >::add_a_mul ( T  a,
small_matrix< T > &  A,
small_matrix< T > &  B 
) [inline]

Operation 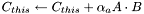$ C_{this} \leftarrow C_{this} + \alpha_{a} A \cdot B$.

The matrices should have the consistent sizes. A and B may coincide, but may not coincide with *this. The function returns the reference to 'this'.

template<class T>
small_matrix< T > & small_matrix< T >::transposed ( small_matrix< T > &  A  )  [inline]

Transpose a given matrix and save the result to 'this' one: 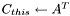$ C_{this} \leftarrow A^{T}$.

The matrices should have the corresponding sizes. That may be a reference to the same matrix which should be square. But transposed () is a bit more efficient in this case. A reference to 'this' matrix is returned.

template<class T>
small_matrix< T > & small_matrix< T >::transposed (  )  [inline]

Transposes 'this' matrix: $ C_{this} \leftarrow C_{this}^{T} $.

The matrix must be square.

template<class T>
small_matrix< T > & small_matrix< T >::conjugate ( small_matrix< T > &  A  )  [inline]

Compute the conjugate of a given matrix and save the result to 'this' one: 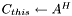$ C_{this} \leftarrow A^{H}$.

The matrices should have the corresponding sizes. That may be a reference to the same matrix which should be square. But conjugate () is a bit more efficient in this case. A reference to 'this' matrix is returned.

template<class T>
small_matrix< T > & small_matrix< T >::conjugate (  )  [inline]

Computes a conjugate of 'this' matrix, returns the reference to it: 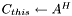$ C_{this} \leftarrow A^{H}$.

The matrix must be square.

template<class T>
small_matrix< T > & small_matrix< T >::invmul_Gauss ( small_matrix< T > &  M1  )  [inline]

Operation: 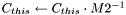$ C_{this} \leftarrow C_{this}\cdot M2^{-1}$.

The calculation is done by the Gaussian elimination with pivoting. As the pivote element, the first nonzero element in the current column is taken. If no nonzero pivote elements found (i.e. this is numerically singular), the function throws an exception. The contents of this is always destroyed. The function returns the reference to 'this' matrix.

template<class T>
void small_matrix< T >::LU_decomp ( small_matrix< T > *  inv_L = 0  )  [inline]

Computes the complete LU-decomposition of a matrix, i. e. :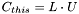$ C_{this} = L \cdot U$.

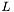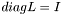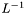$L$ is a lower diagonal matrix, $U$ is an upper diagonal matrix, $diag L = I$. The function returns $U$ in 'this' matrix and $L^{-1}$ as inv_L (unless inv_L == 0). If the complete LU-decomposition does not exist, the function throws an exception.

template<class T>
small_matrix< T > & small_matrix< T >::mul_by_Givens ( small_matrix< T > &  M1  )  [inline]

Multiply 'this' matrix (M2) by the Givens rotation transforming a given matrix (M1) to an upper triangular form.

After the operation M1 contains the upper triangular form. The function returns the reference to 'this' matrix:

template<class T>
small_matrix< T > & small_matrix< T >::invmul_Givens ( small_matrix< T > &  M1  )  [inline]

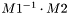Multiplyes 'this' (M2) matrix by $M1^{-1}$, thus computes the product $M1^{-1} \cdot M2$.

This is done by the Givens rotations. The result is stored in M2. The contents of M1 is always destroyed. If the matrix M1 is not invertable by the QR decomposition (i. e. it is a singular matrix) then the function throws an exception. The contents of the matrices M1 and M2 is then destroyed.

template<class T>
void small_matrix< T >::QR_Givens ( small_matrix< T > &  M  )  [inline]

Computes the QR-decomposition by the Givens rotations.

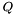The matrix to decompose should be in $M$. The function saves the upper triangular matrix $R$ in $M$ whereas the transformation $Q$ is saved in 'this'. The 'this' matrix should have the same size as $M$.

template<>
float small_matrix< float >::conj ( float  x  )  [inline]

template<>
double small_matrix< float >::abs ( float  x  )  [inline]

template<>
double small_matrix< float >::sc_square ( float  x  )  [inline]

template<>
bool small_matrix< float >::is_num_zero ( float  x  )  [inline]

Member Data Documentation

template<class T>
int small_matrix< T >::m [protected]

number of the rows

template<class T>
int small_matrix< T >::n [protected]

number of the columns

template<class T>
T* small_matrix< T >::entry [protected]

array of the entries

The documentation for this class was generated from the following files:
Generated on Fri Sep 21 12:34:36 2007 for SG2 by  doxygen 1.5.2