small_matrix.hpp File Reference

Header for computations with small dense matrices. More...

#include <cmath>
#include <cstring>
#include <iostream>
#include "small_m_ex.hpp"

Include dependency graph for small_matrix.hpp:

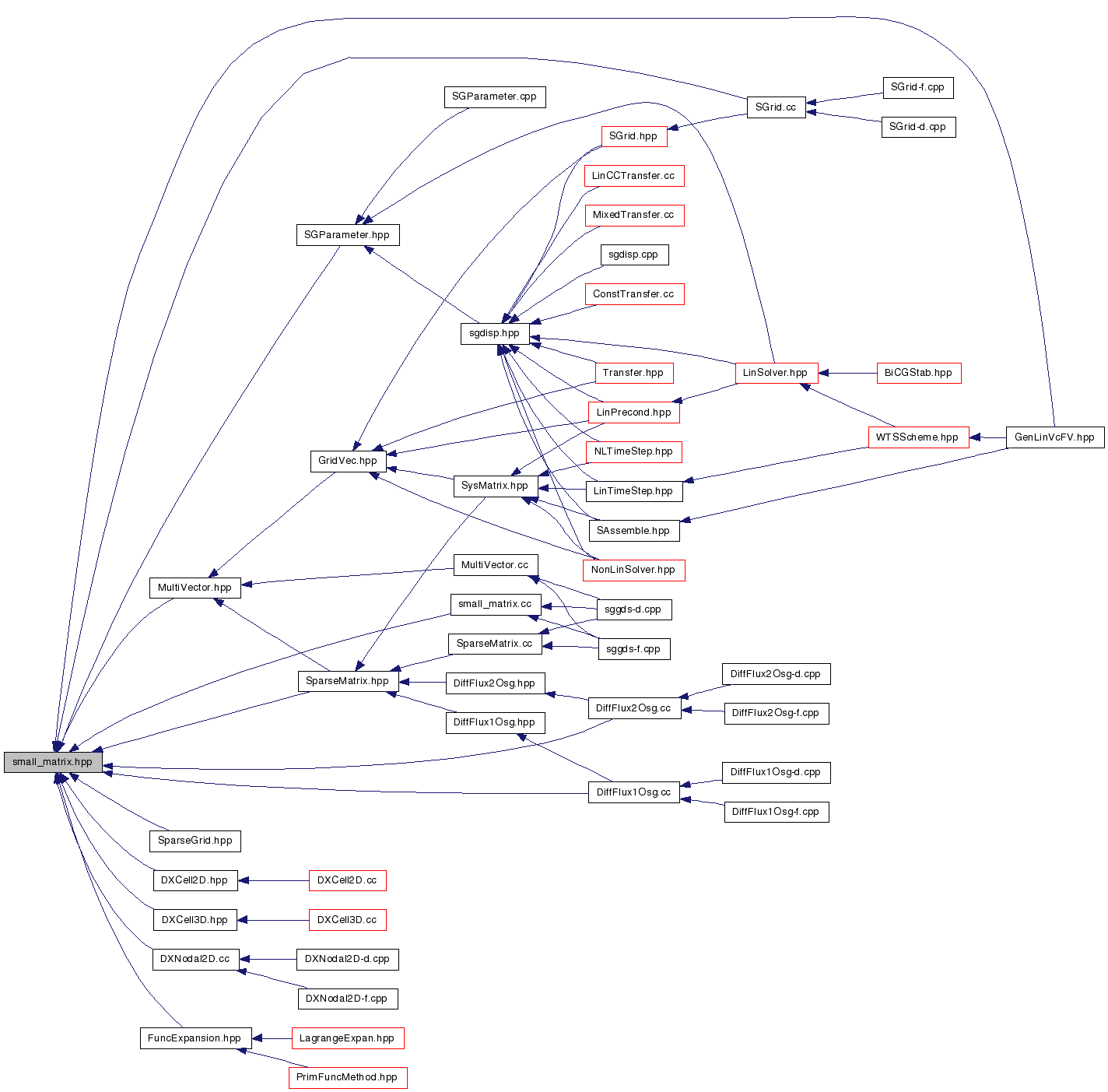
This graph shows which files directly or indirectly include this file:


Classes
class	small_matrix< T >
	The low-level class for small dense matrices. More...
class	small_vector< T >
	A synonym for small_matrix<T> having only one constructor (that with one size). More...
class	SmallMatrix< T >
	High-level class for small matrices and small vectors. More...
Defines
#define	DCL_SMALL_MATR(T, matr_name, m, n)
#define	DCL_SMALL_VECT(T, vec_name, m)
Functions
template<class T>
std::ostream &	operator<< (std::ostream &s, small_matrix< T > &A)
	Print a matrix in the raw form.
template<class T>
SmallMatrix< T >	operator+ (small_matrix< T > &A, small_matrix< T > &B)
template<class T>
SmallMatrix< T >	operator- (small_matrix< T > &A, small_matrix< T > &B)
template<class T>
SmallMatrix< T >	operator * (small_matrix< T > &A, small_matrix< T > &B)
template<class T>
SmallMatrix< T >	operator * (small_matrix< T > &A, T a)
template<class T>
SmallMatrix< T >	operator * (T a, small_matrix< T > &A)
template<class T, class S>
void	convert (small_matrix< T > &from, small_matrix< S > &to)
	Converts an object of small_matrix<T> to small_matrix<S>.
template<class T, class S>
void	Convert (small_matrix< T > &from, SmallMatrix< S > &to)
	Converts an object of small_matrix<T> to SmallMatrix<S>.
template<class T>
void	sym_Householder_tridiag (small_matrix< T > &A, small_matrix< T > &B)
	Householder tridiagonalization method for symmetric matrices.
template<class T>
bool	sym_eig_QR (small_matrix< T > &A, small_matrix< T > &S, int eig_QR_moi=128, double eig_QR_prec=5e-14)
	Computes eigenvalues and the corresponding eigenvectors of the matrix A by the QR-method.
template<class T>
small_matrix< T > &	operator/= (small_matrix< T > &B, small_matrix< T > &A)
	Operation 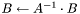$B \leftarrow A^{-1} \cdot B$ .
template<class T>
T	det (small_matrix< T > const &A)
	Returns the determinant of a given matrix.

Detailed Description

Header for computations with small dense matrices.

This file provides tools for handling small dense matrices either kept in a two-dimentional array (the rows of the matrix are then subarrays in the array) or described as objects by means of these tools. Small vectors are treated as one-column matrices.

There are two classes: small_matrix (with a synonym small_vector for the declaration of column vectors) and SmallMatrix. Use small_matrix (and small_vector) if you already have a matrix (vector) with entries in a array or if you declare this array as an (for ex. automatic) variable in your procedure. This class does not initiate any implicit dynamic allocation of memory and contains only functions that can save the computation time. You can also use macros DCL_SMALL_MATR and DCL_SMALL_VECT to declare both the array and the matrix (or vector). This class provides high computational efficiency and should be prefered. But you cannot expect it to be convinient because, for ex. you cannot use its objects in arithmetical expressions. (Nevertheless, assignments like "+=", ... are impelemted.)

The class SmallMatrix provides a high-level mechanism for handling small matrices. It allocates the memory automatically and contains the usual arithmetical operations. Note however that the arithmetical expressions implicitly create new matrices and are therefore slow. Note that both the classes are completely compatible, so that you can mix them.

Both the classes are templates. You can substitute for 'T' any type that satisfies the following conditions (which are satisfied for 'float' and 'double'):

a) this is an arithmetic type, i.e. the operations +, -, *, / are
well-defined for it; b) the zero (the additive unit) for T is the physical zero in all the bytes; c) assignement means merely copying of the bytes and can be done by memcpy; d) the following functions are implemented:

T small_matrix<T>::conj (T x) is the conjugate for x
(for double and float it is merely x);
double small_matrix<T>::abs (T x) is the absolute value of x
(for double and float it is fabs (x));
double small_matrix<T>::sc_square (T x) is the product of x and
conj (x) casted to 'double' (for the Eucleadean norm);
bool small_matrix<T>::is_num_zero (T x) returns true if x is
the numerical zero (i.e. very small); for double and float this
is merely a comparison of fabs (x) with a small number (s. below).
All these functions are 'static' and can be called using for ex.
small_matrix<double>::is_num_zero (x); Besides, they are 'inline'.
<< for T for the output.

There is also the function 'convert' for converting small_matrix<T> to small_matrix<S> for different types 'T' and 'S'. This matrix requires the well-defined assignment operation 'S = T' and the matrices of the same size. You can also convert an object of small_matrix<T> to an object of SmallMatrix<S> using 'Convert'. Then the sizes of the destination object are set automatically, but a memory allocation is involved.

Error handling: The functions are implemented to use the exeption mechanism at computational problems. Nevertheless there is no unified exception type. Instead you must write a file small_m_ex.hpp that defines the following macros for the exception expression in a 'throw' operator: SMALL_MAT_NO_MEMORY to indicate a lack of memory, SMALL_MAT_SINGULAR_INV(m) to indicate inversion of a singular matrix, SMALL_MAT_SIZE_MISMATCH(m) to indicate matrix size inconsistencies, SMALL_MAT_GEN_ERROR(m) for general computation errors. Here 'm' is a text message (of type 'char *') with the error description.

Numerical methods implemented for these representation of matrices:

As member functions:
- M.compute_det () - computes det M (using a QR-decomp.), destroys M,
- M2.invmul_Gauss (M1) computes $M1^{-1}\cdot M2$ using the Gaussian elimination,
- LU_decomp - computes the complete LU-decomposition,
- mul_by_Givens - computes the Givens rotation,
- M2.invmul_Givens (M1) computes $M1^{-1} \cdot M2$ using the Givens rotations,
- QR_Givens - computes the QR-decomposition using the Givens rotations.
As non-member functions:
- sym_Householder_tridiag - tridiagonalization by the Householder reflections,
- sym_eig_QR - solves symmetric eigenvalue problems (the QR-method).

History: July 2, 2004 - templates

Note:: Indexation fault and size mismatch conditions are only checked if the macro CHECK_ARRAY_RANGE is defined.

Define Documentation

#define DCL_SMALL_MATR	(	T,
		matr_name,
		m,
		n	)

Value:

T matr_name##_entries [m] [n]; \
small_matrix<T> matr_name (m, n, (T *) matr_name##_entries);

The following macro declares both the matrix and an array for it. The sizes of the matrix should be constants (else declare an object of SmallMatrix . For a matrix matr_name, the array is called matr_name_entries.

Parameters:

	T	Type of the elements in the matrix.
	matr_name	Name of the object-variable.
	m	Number of columns.
	n	Number of rows.

#define DCL_SMALL_VECT	(	T,
		vec_name,
		m	)

Value:

T vec_name##_entries [m]; \
small_vector<T> vec_name (m, (T *) vec_name##_entries);

The following macro is the same as the previous one, but declares a column m-vector (a matrix of size m*1). m should be a constant.

Parameters:

	T	Type of the elements in the vector.
	vec_name	Name of the object-variable.
	m	Number of elements.

Function Documentation

template<class T, class S>

void Convert	(	small_matrix< T > &	from,
		SmallMatrix< S > &	to
	)			`[inline]`

Converts an object of small_matrix<T> to SmallMatrix<S>.

The conversion is done by setting the sizes of the SmallMatrix<S> from the original matrix and copying the elements. The assignment S = T should be well-defined. On an error the function throws an exception.

Parameters:

`[in]`	from	Source-matrix.
`[in]`	to	Target-matrix.

template<class T, class S>

void convert	(	small_matrix< T > &	from,
		small_matrix< S > &	to
	)			`[inline]`

Converts an object of small_matrix<T> to small_matrix<S>.

The Conversion is done by copying the elements. Two following conditions should be satisfied:

Both the objects should exist and have the same sizes.
The assignment S = T should be well-defined. On an error the function throws an exception.
Parameters:

[in] from Source-matrix.

[in] to Target-matrix.

template<class T>

T det ( small_matrix< T > const & A ) [inline]

Returns the determinant of a given matrix.

The computation but does not destroy the matrix.

Note:: Uses compute_det

template<class T>

SmallMatrix<T> operator *	(	T	a,
		small_matrix< T > &	A
	)			`[inline]`

template<class T>

SmallMatrix<T> operator *	(	small_matrix< T > &	A,
		T	a
	)			`[inline]`

template<class T>

SmallMatrix<T> operator *	(	small_matrix< T > &	A,
		small_matrix< T > &	B
	)			`[inline]`

template<class T>

SmallMatrix<T> operator+	(	small_matrix< T > &	A,
		small_matrix< T > &	B
	)			`[inline]`

template<class T>

SmallMatrix<T> operator-	(	small_matrix< T > &	A,
		small_matrix< T > &	B
	)			`[inline]`

template<class T>

small_matrix<T>& operator/=	(	small_matrix< T > &	B,
		small_matrix< T > &	A
	)			`[inline]`

Operation 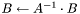$B \leftarrow A^{-1} \cdot B$ .

Computes 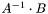$A^{-1} \cdot B$ and saves the result in $B$ not destroying $A$ . The function uses invmul_Gauss and can induce the exceptions. The function returns the reference to $B$ .

template<class T>

std::ostream& operator<<	(	std::ostream &	s,
		small_matrix< T > &	A
	)			`[inline]`

Print a matrix in the raw form.

list the entries in the first line, print '\t', then list the entries of the next line etc.

template<class T>

bool sym_eig_QR	(	small_matrix< T > &	A,
		small_matrix< T > &	S,
		int	eig_QR_moi = `128`,
		double	eig_QR_prec = `5e-14`
	)			`[inline]`

Computes eigenvalues and the corresponding eigenvectors of the matrix A by the QR-method.

The Wilkinson shift strategy is used. Only symmetric matrices are allowed as Wilkinson strategy is implemented only for this case. The matrix 'A' is destroyed, and after the computation it contains an almost diagonal matrix, whose diagonal entries are approximations of the eigenvalues. These entries are ordered in the ascending order. The second argument S contains in its columns the corresponding eigenvectors. The method is iterative and there are two stopping criteria:

if the offdiagonal entries of the Hessenberg form are smaller then
eig_QR_prec or the method has fulfilled eig_QR_moi iterations.
if the required precision has been achieved. In this case the function returns 0
non-zero otherwise.
if the precision has not been achieved after eig_QR_moi iterations. It throws an exception in the case of a matrix-size mismatch.

Note:: Here, 'T' must be an ordered type, i.e. 'double' or 'float'!
For the numerical stability reasons, we advise to use only 'double'.

Parameters:

`[in,out]`	A	The Matrix to solve the eigenproblem for.
`[in,out]`	S	Contains the eigenvectors after the call.
`[in]`	eig_QR_moi	Maximum number of the iterations to do.
`[in]`	eig_QR_prec	The precision to achieve.

template<class T>

void sym_Householder_tridiag	(	small_matrix< T > &	A,
		small_matrix< T > &	B
	)			`[inline]`

Householder tridiagonalization method for symmetric matrices.

Transforms a given matrix A to the tridiagonal form and saves it in B. After the computation A keeps the back transformation.

Note:: Here, 'T' must be an ordered type, i.e. 'double' or 'float'!

Parameters:

`[in,out]`	A	Initially the matrix to tridiagonalize, contains the transformation after the call.
`[in]`	B	For the tridiagonal matrix

Generated on Fri Sep 21 12:33:53 2007 for SG2 by

1.5.2

small_matrix.hpp File Reference

Classes

Defines

Functions

Detailed Description

Define Documentation

Function Documentation