NewtonSolver< T > Class Template Reference

The Newton method class template. More...

#include <NewtonSolver.hpp>

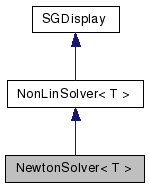
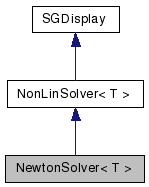
Inheritance diagram for NewtonSolver< T >:

[legend]Collaboration diagram for NewtonSolver< T >:


Public Member Functions
virtual void	PrintParam ()
	Prints the name and parameters of the solver.
virtual void	Run (NonLinSys< T > &p, GridVec< T > &u)
	Solves a given non-linear system.
	NewtonSolver (unsigned the_disp_type, double the_reduction, unsigned the_max_iter, double the_abs_prec, SysMatrix< T > &the_Jac, LinSolver< T > &the_lin_solver, NewtonLineSearch< T > *the_line_search=NULL, T the_damp=1)
	For hard-coded paramters.
	NewtonSolver (SGParam list, SysMatrix< T > &the_Jac, LinSolver< T > &the_lin_solver, NewtonLineSearch< T > the_line_search=NULL)
	Constructor for reading the halting criteria from SG parameters.

Detailed Description

template<typename T>
class NewtonSolver< T >

The Newton method class template.

This class implements the Newton method and similar iterations (like the fixed-point iteration or the Quasi-Newton methods). Which iteration it is, depends on the approximation of the Jacobian computed by the object of the NonLinSys<T> class representing the non-linear system.

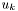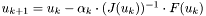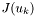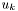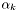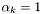For non-linear system $ F (u) = 0 $ , the iteration computes guesses $ u_k $ using the recurrence $u_{k+1} = u_k - \alpha_k \cdot (J (u_k))^{-1} \cdot F (u_k)$ , where $ J (u_k) $ is the approximation of the Jacobian for the guess $ u_k $ and $\alpha_k$ is the damping factor chosen by the line-searche strategy. If no line-search strategy is specifyed, $\alpha_k = 1$ .

Note that in general, the Newton method is not convergent. You need also a line-search strategy. Nevertheless, specification of a line-search strategy is optional.

The templates depend on a type T. This type should satisfy the conditions listed in 'small_matrix.hpp' for small matrices.

Additionally we check whether the damping factor (of type 'T') is equal to '1'. This is done for the efficiency only and it is OK if this condition is always false. But it should be allowed by the syntax. Besides, 1 is the default value of the 'damp' parameter of the Newton solver class.

Constructor & Destructor Documentation

template<typename T>

NewtonSolver< T >::NewtonSolver	(	unsigned	the_disp_type,
		double	the_reduction,
		unsigned	the_max_iter,
		double	the_abs_prec,
		SysMatrix< T > &	the_Jac,
		LinSolver< T > &	the_lin_solver,
		NewtonLineSearch< T > *	the_line_search = `NULL`,
		T	the_damp = `1`
	)			`[inline]`

For hard-coded paramters.

Parameters:

`[in]`	the_disp_type	The display type
`[in]`	the_reduction	The desired reduction (0 to do 'max_iter' iter.)
`[in]`	the_max_iter	The maximum number of iterations
`[in]`	the_abs_prec	The minimum norm of the residual
`[in]`	the_Jac	Matrix hierarchy for the Jacobian
`[in]`	the_lin_solver	The linear solver for the Jacobian
`[in]`	the_line_search	The line search strategy
`[in]`	the_damp	The initial damping factor

template<typename T>

NewtonSolver< T >::NewtonSolver	(	SGParam *	list,
		SysMatrix< T > &	the_Jac,
		LinSolver< T > &	the_lin_solver,
		NewtonLineSearch< T > *	the_line_search = `NULL`
	)			`[inline]`

Constructor for reading the halting criteria from SG parameters.

The parameter names are:

NLReduction - minimal reduction factor for the defect,
NLMaxIter - maximum number of iterations to do,
NLAbsPrec - minimum norm of the residual to achieve,
NLDamp - the initial damping factor for the updates.

Parameters:

`[in]`	list	The list of the parameters
`[in]`	the_Jac	Matrix hierarchy for the Jacobian
`[in]`	the_lin_solver	The linear solver for the Jacobian
`[in]`	the_line_search	The line search strategy

Member Function Documentation

template<typename T>

void NewtonSolver< T >::PrintParam ( ) [inline, virtual]

Prints the name and parameters of the solver.

Implements NonLinSolver< T >.

template<typename T>

void NewtonSolver< T >::Run	(	NonLinSys< T > &	p,
		GridVec< T > &	u
	)			`[inline, virtual]`

Solves a given non-linear system.

Parameters:

`[in]`	p	The non-linear system to solve
`[in]`	u	The initial guess and the solution

Implements NonLinSolver< T >.

The documentation for this class was generated from the following files:

Generated on Fri Sep 21 12:34:23 2007 for SG2 by

1.5.2

NewtonSolver< T > Class Template Reference

Public Member Functions

Detailed Description

template<typename T> class NewtonSolver< T >

Constructor & Destructor Documentation

Member Function Documentation

template<typename T>
class NewtonSolver< T >