SysPrecond< T > Class Template Reference

Base class template of preconditioners for iterative linear solvers for SysMatrix<T> -matrices. More...

#include <LinPrecond.hpp>

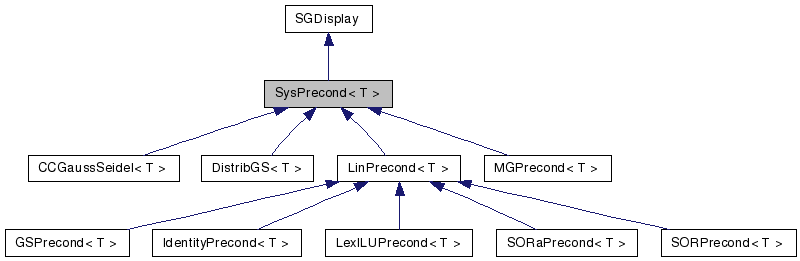
Inheritance diagram for SysPrecond< T >:

Inheritance graph
[legend]
Collaboration diagram for SysPrecond< T >:

Collaboration graph
[legend]
List of all members.

Public Member Functions

virtual void PrintParam ()=0
 Prints the name of the preconditioner and (optionally) the parameters.
virtual void PreProcess (SysPrecondCtxt &context, SysMatrix< T > &A)=0
 Prepares the preconditioner for a given matrix hierarchy.
virtual void Run (SysPrecondCtxt &context, GridVec< T > &r, GridVec< T > &c)=0
 Applies the preconditioner to a given vector 'r', i.e. computes 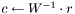$c \leftarrow W^{-1} \cdot r$.
virtual void PostProcess (SysPrecondCtxt &context)=0
 Releases the memory allocated in PreProcess, ...
virtual ~SysPrecond ()
 Virtual destructor.

Detailed Description

template<typename T>
class SysPrecond< T >

Base class template of preconditioners for iterative linear solvers for SysMatrix<T> -matrices.

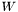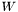A preconditioner $W$ is an easily invertable matrix that approximates the system matrix $A$. The class provides the routines for inverting $W$. This file contains the declarations of base classes for elementary preconditioners for the SparseMatrix<T> -matrices as well as the composite preconditioners for SysMatrix<T> -matrices.

Note that the base class for preconditioners for SparseMatrix<T> -matrices is derived from that for SysMatrix<T> -matrices. Due to this construction you can use the elementary preconditioners directly in the linear solvers for SysMatrix<T> -matrices. Such a preconditioner is the block-Jacobi method that uses the elementary preconditioners on the blocks.

How to use the preconditioners:
This is the same for both the classes. We describe it for SysPrecond . Let MyPrecond<T> be a class derived from SysPrecond<T> . First, create an object of the class MyPrecond<T> . This may require specification of preconditioner-dependent parameters (like those for the SOR-method etc.): MyPrecond<double> precond (<parameters>); As soon as you have a system matrix to apply the preconditioner to, prepare 'precond' to work with this matrix by calling 'PreProcess'. It fills the 'preconditioner context':

SysPrecondCtxt precond_ctxt;
...
precond.PreProcess (precond_context, A);

The preconditioner saves the data computed for this matrix in the context. (E.g. this can be the triangular matrices in the case of the ILU-methods.) Then pass the context every time you call the preconditioner:

precond.Run (precond_ctxt, r, c);

When you are done with the matrix, you must release the data allocated by the preconditioner:

precond.PostProcess (precond_ctxt);

Note that the context referes to the preconditioner object and the given matrix. So neither the preconditioner object nor the matrix may be changed/destroyed until the context is released by the 'PreProcess'. Usually what you need is to declare a preconditioner object and initialize it with the parameters. Then you pass a reference to this object to a linear solver (like the CG-method) that creates the preconditioner contextes itself whenever it needs. For the elementary preconditioner the context is just a void-pointer.

How to programme a new preconditioner:
Derive a subclass of SysPrecond<T> and write implementations for 'PrintParam', 'PreProcess', 'Run' and 'PostProcess'. In 'PreProcess' set the reference to you preconditioner and compute the additional information (or at least, save the reference to the system matrix - cf. Remark below) in the preconditioner context.

The templates depend on a type T. This type should satisfy the conditions listed in small_matrix.hpp for small matrices.

Note:

  1. Only PreProcess gets the matrix hierarchy as an argument. This function prepares the routines to approximately invert the fine grid matrix. Nevertheless the other routines (Run and PostProcess) may need this hierarchy, too. Thus, the hierarchy must be kept unchanged until you call PostProcess and you may save a reference to it in the preconditioner context.
  2. Normally the preconditioner does not need to output anything. We obey further the following rule: The routine 'Run' prints nothing on SG_DISP_NO and SG_DISP_RED, and prints the name with the parameters on SG_DISP_FULL. (The greater values of the type can be used for debugging.)

Constructor & Destructor Documentation

template<typename T>
virtual SysPrecond< T >::~SysPrecond (  )  [inline, virtual]

Virtual destructor.

Member Function Documentation

template<typename T>
virtual void SysPrecond< T >::PrintParam (  )  [pure virtual]

Prints the name of the preconditioner and (optionally) the parameters.

Implemented in CCGaussSeidel< T >, DistribGS< T >, GSPrecond< T >, LexILUPrecond< T >, IdentityPrecond< T >, MGPrecond< T >, SORPrecond< T >, and SORaPrecond< T >.

template<typename T>
virtual void SysPrecond< T >::PreProcess ( SysPrecondCtxt &  context,
SysMatrix< T > &  A 
) [pure virtual]

Prepares the preconditioner for a given matrix hierarchy.

This function must be called only once for a given matrix hierarchy. then the preconditioner can be applied to any residual and any right-hand side. This function does not return any value but may throw exceptions

Parameters:
[in] context The context to initialize
[in] A The system matrix hierarchy

Implemented in CCGaussSeidel< T >, DistribGS< T >, and MGPrecond< T >.

template<typename T>
virtual void SysPrecond< T >::Run ( SysPrecondCtxt &  context,
GridVec< T > &  r,
GridVec< T > &  c 
) [pure virtual]

Applies the preconditioner to a given vector 'r', i.e. computes 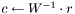$c \leftarrow W^{-1} \cdot r$.

Note:
In some cases 'c' and 'r' must be physically different vectors, but they should have equal sizes. This function does not return any value but may throw exceptions.
Parameters:
[in] context The context for the preconditioner
[in] r The residual
[in] c The correction

Implemented in CCGaussSeidel< T >, DistribGS< T >, and MGPrecond< T >.

template<typename T>
virtual void SysPrecond< T >::PostProcess ( SysPrecondCtxt &  context  )  [pure virtual]

Releases the memory allocated in PreProcess, ...

After you have called this function the preconditioner cannot work before you call PreProcess again. This function does not return any value but may throw exceptions:

Parameters:
[in] context The context to release

Implemented in CCGaussSeidel< T >, DistribGS< T >, LexILUPrecond< T >, LinPrecond< T >, IdentityPrecond< T >, MGPrecond< T >, and SORaPrecond< T >.

The documentation for this class was generated from the following file:
Generated on Fri Sep 21 12:34:41 2007 for SG2 by  doxygen 1.5.2